不正確な説明
「早く解くことができる問題の集まりP」と「ずっと学者が早い解き方を考えているけどいまのところ見つかってなくて、早く解くのが難しい問題の集まりNP」(この定義は正しくない)があって、それは同じ集まりではない(P≠NP)ということを予想したのがP≠NP予想。仮にP=NPだった場合、NPの問題にも実は早い解き方があることになる。
難しい説明
まず、「早く解く」ことを定義すると
多項式時間で解くことができる
となる。
多項式時間で解くとは「問題の大きさをnとしたときに問題を解くのにかかる時間がnの多項式になるもの」のこと。
注1:ここでの時間は問題を解くのに必要とする操作の回数。足すとか引くとか数字の大きさを比較する、などの操作で一回。秒や分の単位はつかない。
注2:問題の大きさがnとしたときに解くのにかかったのがの場合、多項式時間で解けたことになる。
の場合、多項式時間では解くことができないとなる。
なぜ多項式時間で早い遅いを決めるかというと
・実際にパソコンとストップウォッチで測って速さを求めると、性能や状況などでバラツキが出てしまい比較の際に不便
・多項式時間で解けると、問題の大きさnがすごく大きくなったときに
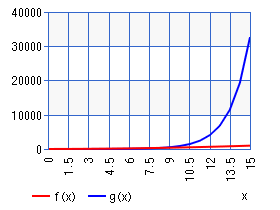
(
でプロットした)
となるので、問題が大きくなった場合でも早く解くことができる。
次に、Pの定義は
Pとは多項式時間(polynomial time)で解ける判定問題の集合である
『Wkipedeia』
となる。
注:判定問題(決定問題)とは答えがyes/noになる問題のこと
そして、NPの定義は
yes となる証拠が与えられたとき、その証拠が本当に正しいかどうかを多項式時間で判定できる問題。
簡単に言い換えると「誰かが問題の答えとしてなにかを出したときに、本当にそれが正しいかどうかを多項式時間で確認ができる問題」となる。
注:多項式時間で問題を解けるかどうかは定義に含まれない。答えの確認を多項式時間できるかどうかだけ。
Pには属さずNPに属する問題の例としては一筆書きがある。
当然、Pに属する問題は(多項式時間で解けるならばある答え正しいかどうかを多項式時間で確認ができるので)NPにも属する。
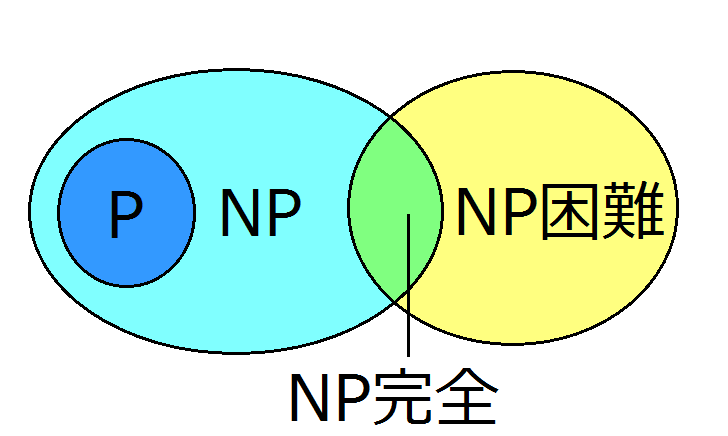
仮にP=NPだった場合、NPに属する問題が多項式時間で解く方法があるということになり、結果的に巡回セールスマン問題を解くことにつながる。